Coeficiente de correlación lineal de Pearson
El coeficiente de correlación de Pearson, pensado para variables cuantitativas (escala
mínima de intervalo), es un índice que mide el grado de covariación entre distintas
variables relacionadas linealmente. Adviértase que decimos "variables relacionadas
linealmente".
Esto significa que puede haber variables fuertemente relacionadas, pero no
de forma lineal, en cuyo caso no proceder a aplicarse la correlación de Pearson. Por
ejemplo, la relación entre la ansiedad y el rendimiento tiene forma de U invertida;
igualmente, si relacionamos población y tiempo la relación será de forma exponencial.
En estos casos (y en otros muchos) no es conveniente utilizar la correlación de Pearson.
Insistimos en este punto, que parece olvidarse con cierta frecuencia.
El coeficiente de correlación de Pearson es un índice de fácil ejecución e, igualmente, de
fácil interpretación. Digamos, en primera instancia, que sus valores absolutos oscilan
entre 0 y 1. Esto es, si tenemos dos variables X e Y, y definimos el coeficiente de
correlación de Pearson entre estas dos variables como xy r entonces:
Hemos especificado los términos "valores absolutos" ya que en realidad si se contempla
el signo el coeficiente de correlación de Pearson oscila entre –1 y +1.

No obstante ha de
indicarse que la magnitud de la relación vienen especificada por el valor numérico
del coeficiente, reflejando el signo la dirección de tal valor. En este sentido, tan fuerte
es una relación de +1 como de -1. En el primer caso la relación es perfecta positiva y en
el segundo perfecta negativa. Pasamos a continuación a desarrollar algo más estos
conceptos.
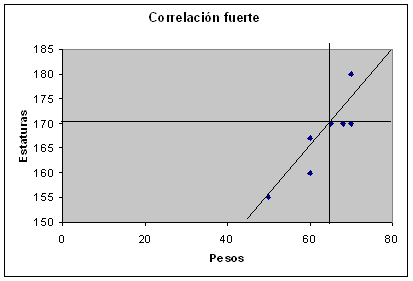
Decimos que la correlación entre dos variables X e Y es perfecta positiva cuando
exactamente en la medida que aumenta una de ellas aumenta la otra. Esto sucede
cuando la relación entre ambas variables es funcionalmente exacta. Difícilmente ocurrirá
en psicología, pero es frecuente en los ciencias físicas donde los fenómenos se ajustan a
leyes conocidas, Por ejemplo, la relación entre espacio y tiempo para un móvil que se
desplaza a velocidad constante. Gráficamente la relación ser del tipo: